En el Día Internacional de las Mujeres en Matemáticas les compartimos la historia de Margherita Beloch Piazzolla, una pionera en trabajar la noción de plegado en el mundo de las matemáticas. Hay mucho material en la web por lo que sólo nos remitimos a contar brevemente que fue la primera en descubrir una de las 7 bases (o tal vez 8) matemáticas del origami conocidas también como axiomas del origami. Estas bases fueron descubiertas simultáneamente por diferentes matemáticos como Koshiro Hatori y Jacques Justin a partir de 1986. Sin embargo una de ellas ya había sido descubierta por Margherita Beloch en 1936. Actualmente se conoce como pliegue de Beloch y permite dividir un ángulo dado en tres partes sin el uso de regla ni compás. Es notable que haya reparado en esta solución por medio del plegado ya que no era una tema que ocupaba a los matemáticos de la época.
Nos podemos preguntar qué tiene de particular trisectar un ángulo por medio de pliegues, estamos acostumbrados a generar ángulos de 60º, de formar hexágonos y pentágonos plegando. Sin embargo la trisección era una figurita difícil de la matemática. Un ángulo puede dividirse en dos secciones iguales por medio de compás y regla pero no puede trisectarse con estas herramientas euclidianas. Se tardó bastante en demostrar esto y lo sorprendente es que es "el pliegue" la herramienta que permite hacerlo.
Este procedimiento tiene a su vez conexión con otros temas de la matemática como resolver ecuaciones de tercer grado sólo plegando y resolver problemas clásicos como la duplicación de cubo.
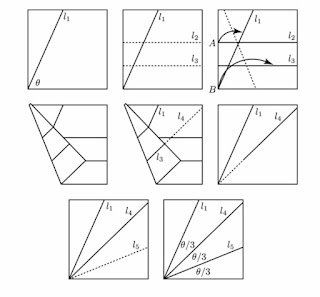
Acompañamos un esquema y les dejamos un video que lo muestra muy claramente.
(este esquema no está visible que la recta L2 puede ser arbitraria pero L3 esta ubicada entre la mitad del borde inferior y L2)
https://mujeresconciencia.com/2017/07/12/margherita-piazzolla-beloch-matematica/